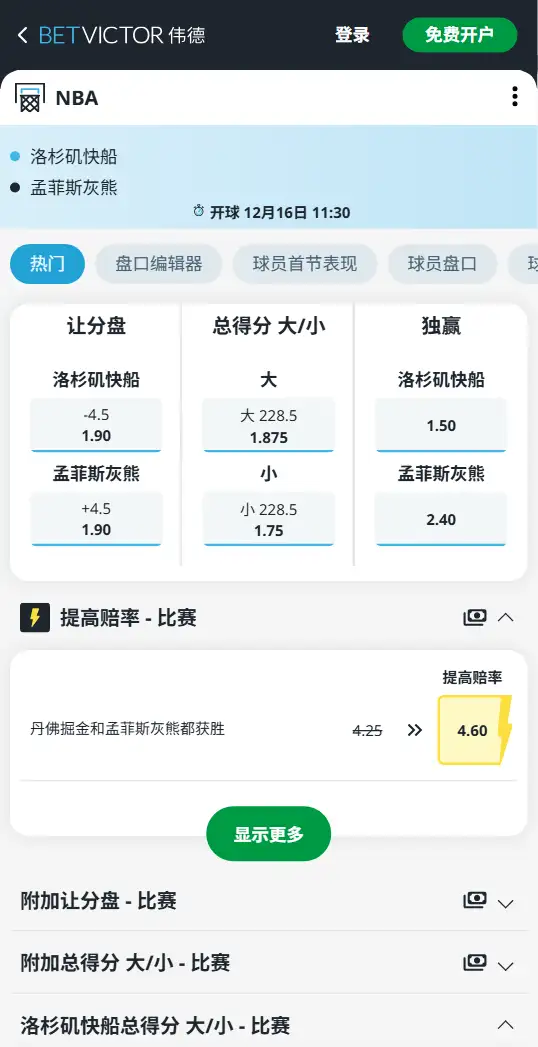
灰熊VS快船,比赛结果

博讯网预测:
- 赢✔️:灰熊 +4.5(约1.89–1.91)
- 赢✔️:小分 228.5(约1.91)
以下是原文
一、比赛背景与形势
12月16日11:30(北京时间),孟菲斯灰熊客场挑战洛杉矶快船,比赛地点为英格尔伍德的Intuit Dome。两队战绩与走势形成明显反差:灰熊目前处在西部中游区间,而快船仍在寻找稳定赢球方式,近期也背负连败压力。
更关键的是,本赛季双方已经有过两次交手,灰熊在系列赛中暂时2-0领先。对快船而言,这场不仅是止跌,更是必须缩小对位劣势的“分水岭”;对灰熊而言,若能客场再下一城,排名与士气都会得到加成。
- 对阵性质:常规赛第三次交锋(本赛季系列赛)
- 心理层面:灰熊占先手,快船需要“扳回一局”
- 赛程层面:快船主场求稳,灰熊客场更看重防守与篮板质量

二、近期表现与实力对比
从近10场表现看,灰熊的稳定性明显更好;快船则在攻防两端都显得“断续”,尤其在关键回合的效率与失误控制上起伏较大。
灰熊近期的赢球逻辑更清晰:防守强度在线、篮板优势明显、轮换里有人能顶上火力缺口;快船的问题则集中在进攻发起的连贯性,以及阵地战效率不足时容易被对手拖进消耗战。
- 灰熊近10场:胜率更高,比赛节奏控制更成熟
- 快船近10场:波动明显,连续性与终结能力不稳
- 数据对照要点:灰熊场均得分不低,但更依赖二次进攻与防守反击;快船整体得分偏保守,且防守端失分并不理想
- 交锋走势:灰熊已在两次交手中占到节奏与对抗优势
- 关键核心:灰熊更靠整体性,快船更依赖球星单打与强解
三、主力伤病与轮换观察
这场灰熊vs快船的轮换变量,主要集中在两队的“中轴线”与“持球发起点”。
灰熊方面,内线人手并不齐整,尤其是中锋位置的缺口,会让他们更依赖小阵容与机动防守;同时替补后场的伤停,会压缩板凳创造力,迫使主力控卫与锋线承担更多组织任务。
快船方面,外线持球核心的出战状态,是盘口波动的最重要触发器之一。一旦主控缺阵或受限,快船会更依赖锋线强解与半场“一个回合一个回合”地磨。
- 灰熊伤停影响点:内线轮换更薄,替补后场可用性下降,可能增加主力上场时间与控球压力
- 快船伤停影响点:后场核心与锋线轮换存在不确定性,进攻端的稳定发起是胜负关键
- 预计首发框架:双方大概率围绕“核心持球 + 双锋线 + 传统中锋/机动内线”展开,但灰熊可能更频繁使用换防与小阵容
四、初盘与即时盘:让分与大小分走势拆解
本场灰熊vs快船的市场节奏很典型:先给主队一定让分优势,随后因伤病与基本面差异出现回调,临近比赛又逐步回到更均衡的区间。
1)让分盘走势
整体来看,让分从“快船让分偏深”逐步向灰熊一侧回落,中间甚至出现较浅让分区间,随后再回到快船让分的主流位置。这种走势通常反映两类信息:
一是早段市场更看重“主场与名气溢价”;二是随着伤病消息与近期战绩对比被消化,资金开始对灰熊的抗衡能力更认可。
- 早盘方向:快船让分开出偏深区间
- 盘中变化:让分一度回落到较浅位置,显示市场对灰熊更“买账”
- 即时主流:让分重新回到快船让分的常见档位(约4.5分附近),分歧仍在
2)大小分走势
总分的变化呈现“先高后压”的特征:开盘给到偏高区间,随后总分一度被压低,临近比赛再回到中高位震荡。结合双方本赛季交手与快船半场进攻的稳定性,这种波动更像是市场在“快船进攻效率是否回升”与“灰熊阵容残缺导致防守质量下降”之间寻找平衡点。
- 初盘总分:开在更高位
- 盘中低点:总分曾被压到更低区间
- 即时主流:回到约228.5附近震荡,市场对节奏与效率仍有分歧
五、比赛对位看点
灰熊想赢,重点在于把比赛拉到他们熟悉的“防守对抗 + 篮板争夺 + 迫使对手打阵地”的节奏;快船想赢,则必须解决两件事:其一是持球端要稳定输出,其二是限制灰熊的二次进攻与转换得分。
- 篮板与二次进攻:灰熊本季篮板端更占优势,快船若让对手反复补篮与外弹三分,比赛会非常难打
- 持球发起稳定性:快船若核心后场状态受限,进攻会出现“卡壳”,被灰熊拖进低效回合
- 犯规与罚球:快船更依赖球星强解制造犯规,灰熊需要控制无谓犯规,避免让对手用罚球续命
- 末节决胜:灰熊更偏整体与纪律性,快船更偏球星硬解,关键回合的选择将直接决定让分与大小分方向
六、让分盘与大小分投注方案
以下方案围绕“灰熊更强的近况稳定性 + 盘口回调逻辑 + 两队交手节奏偏谨慎”来制定,赔率以市场主流欧洲盘面折算的小数赔率呈现(均≥1.50)。
让分盘(主推)
- 灰熊 +4.5(约1.89–1.91)
思路:灰熊近况更稳,且盘口从偏深让分回落后再回升,说明市场对快船“稳胜穿盘”并不一致。灰熊只要把比赛拖进对抗节奏,末节具备咬分能力。
大小分(主推)
- 小分 228.5(约1.91)
思路:总分经历“高开后压”的过程,说明市场并不完全认可这场会打成持续对攻。快船若进攻端仍偏断续,灰熊又更愿意打半场消耗,小分的容错会更高。
备选思路(更稳健的临场观察)
- 若快船后场核心最终缺阵或明显受限:小分优先级继续上升
- 若临场总分再次被抬升到更高区间:小分可考虑分批进场(以更高分界线换取更安全空间)