你是否好奇,一场比赛中双方交换领先地位的频率到底有多高?为什么我们凭直觉下注时常常判断失误?本文通过掷硬币的概率模型,揭示体育比赛中领先交替和平局出现的真实规律,帮助你跳出直觉陷阱,做出更理性、更有价值的投注决策。
而领先地位往往会在双方之间频繁交替。你是否曾思考过,这种领先交换的频率到底有多高?
如果你习惯凭直觉下注,那么你可能错过了比赛背后真正的数学逻辑。
继续阅读,看看为什么直觉常常带你走错方向——以及如何用概率的眼光,更理性地做出判断。
理解概率智慧
从决定是否带伞出门,到赛前下注,我们每天都在根据自己对概率的理解做出各种决策。然而,我们天生的直觉往往不够可靠,甚至会将我们引入误区。此时,统计学数据才是我们最值得信赖的指南,帮助我们回归事实的轨道。
⚠️ 警告:本文揭示的心理误区极具反直觉性,甚至会令经验丰富的统计学家都感到惊讶。但在深入探讨理论之前,我们不妨先做一个小测试,挑战一下你的直觉。
想象一场比赛:两位实力相当的斯诺克选手展开对决。你认为,比赛过程中他们会互相交换领先地位多少次?
你觉得——比赛越久,领先地位交换次数越多,还是越少?
既然假设两位选手实力完全对等,我们可以使用经典的随机模拟方法来理解比赛走势:掷硬币。设定一位选手为正面,另一位为反面,每局胜负完全随机,就像一枚公平的硬币落地。
但要注意:领先地位交换并非每局都可能发生,只有落后的一方先追平比分,领先才有机会转移。
回到核心问题:在这样一场完全对称的比赛中,“平分秋色”的概率究竟多大?
我们借助一个简单而强大的工具——掷硬币实验,用统计学视角揭开直觉误区。
设想掷硬币六次。直觉告诉我们,连续六次正面或反面非常罕见。事实上,掷六次硬币一共可能产生64种组合,而“全为正面”或“全为反面”只有两种,概率为 3.125%。
虽然每次掷出正面或反面的概率都是50%,但这并不意味着在六次试验中一定会出现“三次正面三次反面”的平均分布。
事实上,小样本波动普遍,极端结果(如5:1或6:0)出现概率远高于直觉预期。
计算均等概率
在连续掷硬币实验中,正面(H)和反面(T)出现次数完全相等的概率到底有多大?每次抛掷结果不是正面多,就是反面多,或者刚好相等。注意,只有偶数次掷硬币时,正反面次数才可能相等。
很多人理所当然地认为,随着掷币次数增加(2次、4次、6次……),正反面相等的概率也会上升。
这种想法源自直觉的“平均法则”——认为样本数量增大,结果将趋近总体平均值。但严格统计学告诉我们,这种想法不但不准确,甚至是大错特错。
在《Taking Chances》一书中,数学家 John Haigh 深入研究了独立且公平掷硬币序列中,任意时刻正反面次数恰好相等的概率。这个看似简单的问题,揭示的统计现象足以颠覆直觉。
| 正面(H)与反面(T)次数完全相同的概率 | |||||
|---|---|---|---|---|---|
| 掷硬币次数 | 2 | 4 | 6 | 8 | 10 |
| 分数形式 | 1/2 | 3/8 | 5/16 | 35/128 | 63/256 |
| 概率(%) | 50% | 37.5% | 31.25% | 27.34% | 24.61% |
数据极其反直觉,甚至资深数学家都需反复确认。我们看到,随着掷硬币次数增加,正反面完全相等概率反而下降。
假设连续掷 20 次硬币,问题来了:
在哪一次掷币后,正反面次数最后一次相等?
可能答案包括第 2、4、6……18、20 次,共 11 种。你会选最接近结尾?最早?还是接近中间?
这种直觉再次误导我们。
著名统计学家 David Blackwell 发现,在20次掷币序列中,“最后一次正反面相等”发生的位置从两端向中间对称分布。
换句话说:
- 第 4 次 和第 16 次 出现“最后一次相等”的概率相同;
- 第 0 次(即开始)和第 20 次,概率最高;
- 正中间(如第 10 次)发生概率最低。
这种“钟形对称”分布与我们期望的“随机等分”截然不同,说明:
在概率面前,直觉往往靠不住。
| 掷20次硬币中,最后一次正反面相等时间点分布 | ||||||
|---|---|---|---|---|---|---|
| 时间点 | 0或20 | 2或18 | 4或16 | 6或14 | 8或12 | 10 |
| 概率 | 17.62% | 9.27% | 7.36% | 6.55% | 6.17% | 6.06% |
换言之,如果早期没出现均等现象,可能要等很久才会再发生。
双方交替领先的频率有多高?
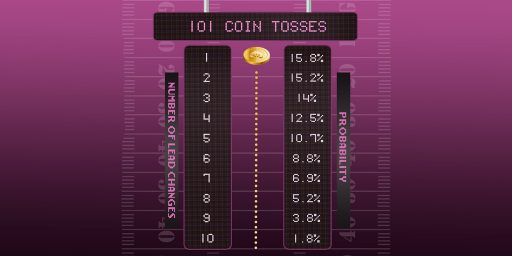
关于领先交换频率,以下是掷101次硬币序列中,领先地位交换次数概率分布:
| 交换次数 | 概率 |
| 0 | 15.8% |
| 1 | 15.2% |
| 2 | 14% |
| 3 | 12.5% |
| 4 | 10.7% |
| 5 | 8.8% |
| 6 | 6.9% |
| 7 | 5.2% |
| 8 | 3.8% |
| 9 | 2.7% |
| 10 | 1.8% |
| 11 | 2.6% |
在双方实力相当、模拟为“掷硬币”的比赛中,领先地位交换并不像很多人想象的那么频繁。
- 领先地位交换不超过4次的概率高达68%;
- 交换5至9次概率约为27%;
- 交换10次或以上概率仅约为4%-5%。
这对许多人来说是惊讶的结果,因为我们往往认为势均力敌的对抗会出现“你追我赶”的激烈拉锯。但数学模型告诉我们,大多数比赛不会频繁出现领先交替。
更令人惊讶的是:在对称随机过程中,比赛后半段有一半时间比分不再回到平局。
换言之:
比赛中点之前领先的一方,往往能保持领先直至结束。
这揭示了随机过程中的“领先惯性”——即使比赛公平且每分独立,一旦建立领先优势,很可能维持到最后。
因此,在博彩或预测时,依赖“感觉局势会翻转”的直觉常常导致误判。
体育博彩中的掷硬币智慧
现在,你应该清楚看到掷硬币实验在体育博彩中的启示。
我们了解到:在势均力敌的对决中,比分达到平局的次数远没有直觉想象中频繁,且这种平局更可能出现在比赛的开头或结尾,而非中段。
例如,统计学家 John Haigh 计算得出,两位实力相当的斯诺克选手在打完前16局时领先的一方,有高达50%的概率持续领先直到第32局结束。这说明前半段领先优势难以被轻易逆转。
那么,这能否应用于足球博彩?
答案是:可以借鉴,但不能完全照搬。足球联赛中的实力差距及变量远比掷硬币模型复杂。因此实际投注需结合联赛结构、战术、赛程等多因素综合分析。
此外,现实中还存在许多掷硬币模型未覆盖的人为因素,例如:
- 损失规避(loss aversion):人们在追求胜利与避免失败时行为模式不同;
- 战术调整与换人策略:比赛中途可能带来巨大变化,掷硬币实验无从体现。
尽管如此,掷硬币作为理论模型,依然为体育博彩者提供宝贵启示:
随机过程中的“领先惯性”、非均匀的平局出现分布、以及直觉失灵现象,都是下注时应重点考虑的因素。
掌握这些概率规律,帮助我们跳出直觉陷阱,做出更理性、更有预期价值的投注决策。